Matahari sebagai Pusat Tata Surya
0
Matahari
merupakan sebuah bintang yang paling dekat dengan bumi. Bintang
merupakan benda langit yang dapat menghasilkan cahaya sendiri Matahari
adalah salah satu dari 100 miliar lebih bintang yang ada di galaksi
Bimasakti. Oleh karena letaknya yang dekat dengan bumi, cahaya matahari
tampak lebih terang dan ukurannya tampak lebih besar dibandingkan dengan
berjuta-juta bintang lainnya. Matahari memancarkan cahaya dan panasnya
karena pada inti matahari terjadi reaksi fusi yang menghasilkan energi
yang sangat besar. Suhu inti matahari ± 15 juta °C dan suhu di permukaan
kurang lebih 6.000 °C, matahari terdiri atas gas hidrogen (80%–90%) dan
gas helium. Energi yang dipancarkan matahari setiap detik setara dengan
energi matahari yang diterima Bumi selama 100 tahun. Panas yang
dipancarkan matahari merupakan sumber energi utama di bumi.
Matahari berputar pada porosnya dari
barat ke timur. Jika dibandingkan dengan bumi, ukuran matahari sangat
besar. Diameter matahari 110 kali diameter bumi. Matahari bentuknya
menyerupai bola gas dengan diameter ±1,4 juta kilometer (1.400.000 km).
Volume matahari hampir 1 juta kali volume bumi. Dengan ukuran matahari
yang sangat besar seperti dijelaskan di atas, maka matahari memiliki
gaya gravitasi yang sangat besar. Gaya gravitasi matahari 28 kali lebih
besar daripada gaya gravitasi bumi. Dengan gaya gravitasi tersebut
terjadi gaya tarik-menarik antara matahari dengan planet-planet dan
benda langit lainnya. Hal ini yang menyebabkan planet-planet dan benda
langit lainnya selalu beredar mengelilingi matahari.
Sumber;mataharibumi2012.blogspot.COM








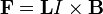
 = perkalian silang vektor, dan
= perkalian silang vektor, dan
















 / 3,14
/ 3,14






